Homework Problem 1
Calculate the magnitude and phase angle of the following complex numbers:
- $13 + 2j$
- $−5 − 3j$
- $−2.4 + 3.6j$
Homework Problem 2
Given the transfer function $G(s) = \frac{2.4}{0.6s^2 + 8s + 36}$, do the following:
- Determine the system output, $y(t)$, for input $u(t) = 30.2 \cos(20t)$.
- Calculate the magnitude of the transfer function at $\omega = 20$ in dB.
- Calculate the time shift between the input and output waveforms at $\omega = 20$
- Generate a Bode plot for the transfer function in Matlab
Homework Problem 3
Given the transfer function $G(s) = \frac{4}{0.2s + 1}$, answer the following:
- What is the cutoff frequency of the transfer function?
- What is the bandwidth of the system represented by the transfer function?
Homework Problem 4
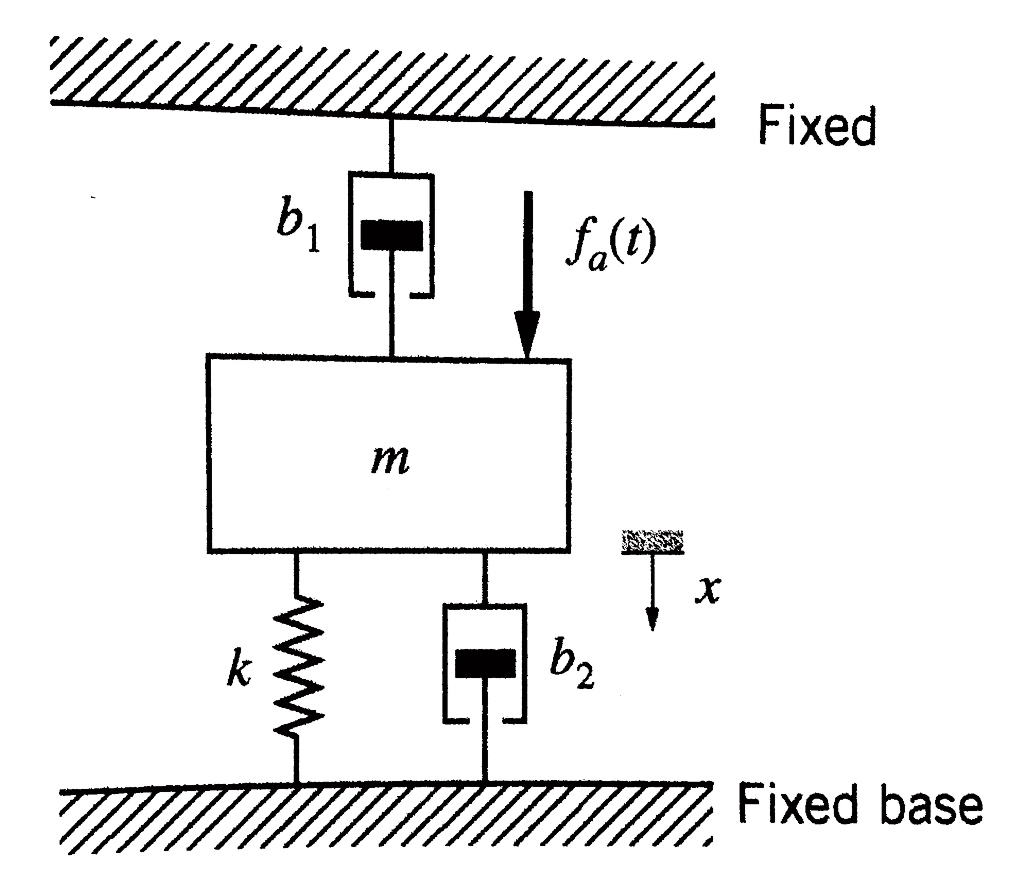
Consider the system shown below. Assume $m = 0.6$ kg, $k = 80$ N/m, $b_1 = 3$ N-s/m, and $b_2 = 0.4$ N-s/m.
- Calculate the output of the system if the input is $f_a(t) = 2 \sin(8t)$ N.
- What input frequency, $\omega$, will cause the largest amplitude of mass displacement?